对主席树的理解以及使用

Posted on | Post modified:

对主席树的理解以及使用

引入

一个长度为$n$的数组，有$m$次查询，每次查询区间$[l,r]$内第$k$小的元素。

如果使用暴力，肯定不可以

使用线段树？可是我只会查询区间最值啊。

那么我们把问题再次简化一下，查询$[1,n]$第$k$小的元素，要求使用线段树来实现。

权值线段树

为了解决这个问题，我们引入一个名词:权值线段树。那么权值线段树是如何解决上面那个问题的呢？

首先，我们对数组进行离散化处理，离散成为$[1,n]$，然后我们建一颗线段树，线段树的节点存放的即为对应区间的数的个数。

比如数组$a={3,3,2,2}$,经过离散化后变为$2,2,1,1$。

对应的线段树即为：

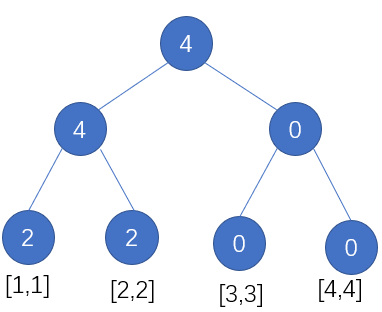
建好线段树之后我们如何求解第$k$小元素呢？我们从根节点出发，看下它的左儿子的元素个数是否超过了$k$，如果超过了$k$，那么第$k$小一定是左儿子的第$k$小，我们直接去访问左儿子，否则，假设左儿子的节点为$num$，那么第$k$小一定是右儿子的第$k-num$小，我们去访问右儿子，直到递归终止，我们便找到了第$k$小元素。

主席树

当我们解决了上一个问题，我们这样考虑：

每输入一个数字$a_i$，就建一棵$[1,i]$的权值线段树，那么如果要查询$[l,r]$的区间第$k$小，直接让这两棵权值线段树做差，然后进行我们上面设计的算法，问题不久迎刃而解了吗？

但是，每建一棵树，这样$n$棵树的空间会达到$O(n^2)$的级别，空间是无法承受的。我们这样想，假设你输入了$a_i$，并且你已经建好了$a_{i-1}$的线段树，是不是$a_i$和$a_{i-1}$的线段树只会有$log$级别的点是不同的，剩下的大部分都是完全一致的。利用这个性质，我们不再开辟新的线段树，而是先把$a_i$会改变掉的节点复制一份，然后对复制的节点进行修改，连接到上次构建好的线段树上，这样我们只用了$log$的空间。最终我们构造的这棵树就叫主席树（其实已经不是一棵树了）。点的个数最多为$O(nlog(n))$。

建立过程

对于数组$a:3,3,2,2$建立主席树:

第一步：离散化为$2,2,1,1$
第二步：输入$2$，构造权值线段树

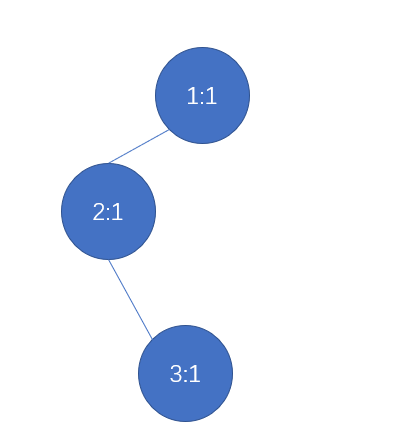
第三步：输入2

2.png

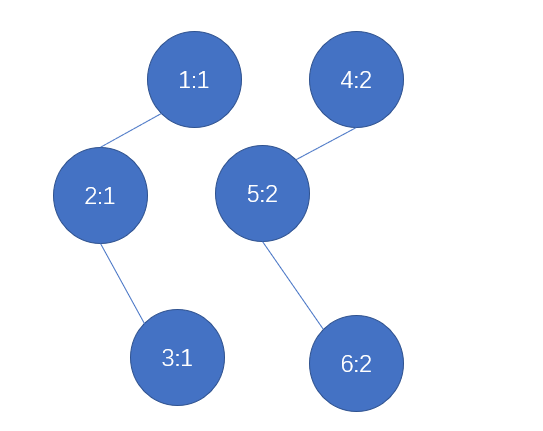
第四步:输入1

3.png

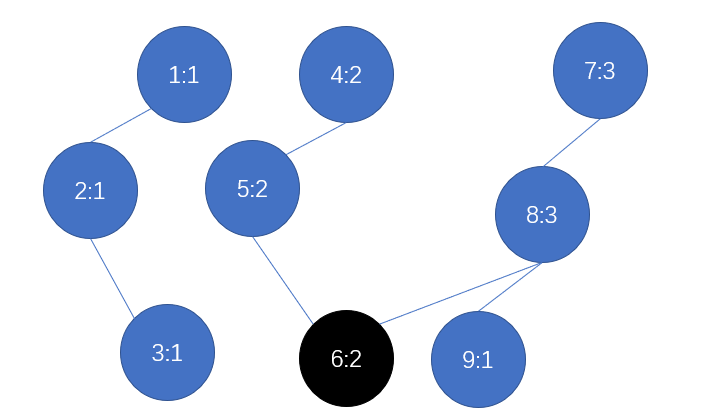
第五步:输入1

4.png

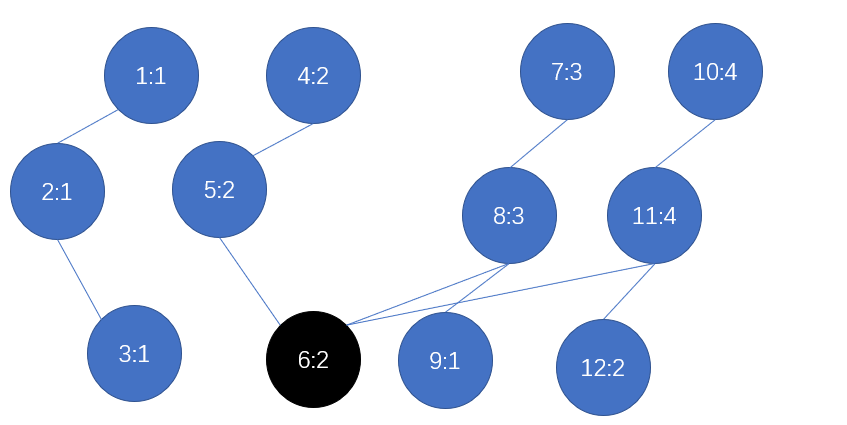
这样我们就构造了一个主席树（有点丑），然后对于要查询的区间$[l,r]$，我们只需要从他们各自的”根”出发，递归做差寻找第$k$大即可。图中四个根分别为$1,4,7,10$。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include<bits/stdc++.h>

using namespace std;
typedef long long ll;

const ll N = 5e5+100;
vector<ll> v;
ll a[N],roots[N],cnt;
struct node{
	ll l,r,num;
}T[N*25];
void update(ll l,ll r,ll &x,ll y,ll pos){
	T[++cnt]=T[y];T[cnt].num++;x=cnt;//复制节点并且更新
	if(l==r) return ;
	ll mid=(l+r)>>1;
	if(mid>=pos) update(l,mid,T[x].l,T[y].l,pos);
	else update(mid+1,r,T[x].r,T[y].r,pos);
}
ll query(ll l,ll r,ll x,ll y,ll k){
	if(l==r) return l;
	ll sum=T[T[y].l].num-T[T[x].l].num;
	ll mid=(l+r)>>1;
	if(sum>=k) return query(l,mid,T[x].l,T[y].l,k);//第$k$小在左子树
	else return query(mid+1,r,T[x].r,T[y].r,k-sum);//在右子树
}
ll getid(ll x){
	return lower_bound(v.begin(),v.end(),x)-v.begin()+1;
}
int main(){
	cnt=0;
	ll n,m;
	scanf("%lld%lld",&n,&m);

	for(ll i=1;i<=n;i++) scanf("%lld",&a[i]),v.push_back(a[i]);
	sort(v.begin(),v.end());

	v.erase(unique(v.begin(),v.end()),v.end());//离散化

	for(ll i=1;i<=n;i++) update(1,n,roots[i],roots[i-1],getid(a[i]));
	while(m--){
		ll l,r,k;
		scanf("%lld %lld %lld",&l,&r,&k);

		printf("%lld\n",v[query(1,n,roots[l-1],roots[r],k)-1]);
	}
	return 0;
}