拉格朗日插值的应用

Posted on | Post modified:

拉格朗日插值的应用

引言：

什么是拉格朗日插值？假设我们现在有三个点 $(x_1,y_1),(x_2,y_2),(x_3,y_3)$，现在我们要找一条唯一的二次曲线刚好经过这三个点。

拉格朗日给出了一个绝妙的方法，他把我们要求的曲线的表达式等同于三个函数的累加。具体是这么操作的：

第一个函数保证$f_1(x_1)=1,f_1(x_2)=f_1(x_3)=0$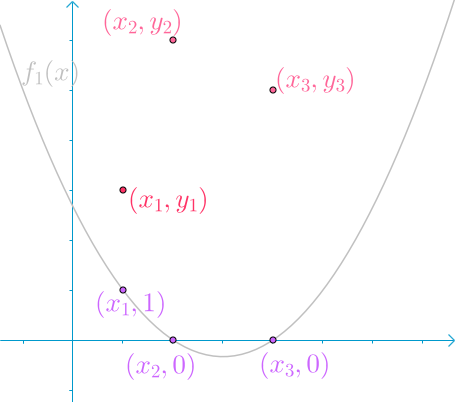
$f_1(x)$
第二个函数保证$f_2(x_2)=1,f_2(x_1)=f_2(x_3)=0$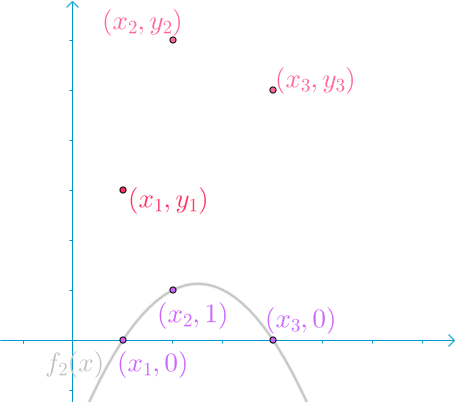
$f_2(x)$
第三个函数保证$f_3(x_3)=1,f_3(x_1)=f_3(x_2)=0$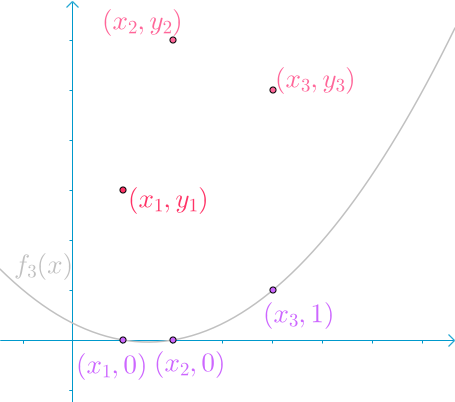
$f_3(x)$
那么我们所要求的函数即为:

$f(x)=y1f_{1}(x)+y2f_{2}(x)+y3f_{3}(x)$
可以保证的是这个函数同时经过$(x_1,y_1),(x_2,y_2),(x_3,y_3)$并且是唯一的满足条件的二次函数。 ## 公式： 如果上面的部分你看懂了，那么你已经掌握了拉格朗日插值的用法和思想。接下来我们要做的就是寻找一个公式使得利用现在已有的$n$个点，来推导出$n-1$次的函数。 那么这个函数为:
$f(x)=\sum_{i=1}^ny_i\prod_{j=1,j\neq i}^n\frac{x-x_j}{x_i-x_j}$

实现：

一般情况下拉格朗日插值的复杂度是$O(n^2)$，即：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include<bits/stdc++.h>

using namespace std;
const int N = 1e6+100;
typedef long long ll;
const ll mod = 998244353;
struct point{
	ll x,y;
}p[N];
int n,k;
ll qpow(ll a,ll b,ll mod){
	ll ans=1;
	while(b){
		if(b&1){
			ans=(ans%mod*a%mod)%mod;
		}
		a=(a%mod*a%mod)%mod;
		b>>=1;
	}
	return ans%mod;
}
ll Lagrange(int k){
	ll ans=0;
	for(int j=1;j<=n;j++){//
		ll base1=1;
		ll base2=1;
		for(int i=1;i<=n;i++){//lj(k)基函数 
			if(j==i) continue;
			base1=(base1%mod*((k-p[i].x)%mod+mod)%mod)%mod;
			base2=(base2%mod*((p[j].x-p[i].x)%mod+mod)%mod)%mod;
		}
		ans=(ans%mod+(p[j].y%mod*base1%mod*qpow(base2,mod-2,mod)%mod)%mod)%mod;
	}
	return ans;
} 
int main(){
	cin>>n>>k;
	for(int i=1;i<=n;i++) cin>>p[i].x>>p[i].y;
	cout<<Lagrange(k)<<endl;
	return 0;
}

如果已知的坐标是连续的话，那么我们可以通过预处理使得复杂度变为$O(n)$,代码以codeforces 622F为例。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include<bits/stdc++.h>

using namespace std;
const int N = 1e6+100;
typedef long long ll;
const ll mod = 1e9+7;
ll p[N],x[N],s1[N],s2[N],ifac[N];
ll qpow(ll a,ll b){
	ll ans=1;
	while(b){
		if(b&1) ans=(ans%mod*a%mod)%mod;
		a=(a%mod*a%mod)%mod;
		b>>=1;
	}
	return (ans%mod+mod)%mod;
}

//拉格朗日插值，n项，每个点的坐标为(x_i,y_i)，求第xi项的值，保证x是连续的一段 
ll lagrange(ll n, ll *x, ll *y, ll xi) {
    ll ans = 0;
    s1[0] = (xi-x[0])%mod, s2[n+1] = 1;
    for (ll i = 1; i <= n; i++) s1[i] = 1ll*s1[i-1]*(xi-x[i])%mod;
    for (ll i = n; i >= 0; i--) s2[i] = 1ll*s2[i+1]*(xi-x[i])%mod;
    ifac[0] = ifac[1] = 1;
    for (ll i = 2; i <= n; i++) ifac[i] = -1ll*mod/i*ifac[mod%i]%mod;
    for (ll i = 2; i <= n; i++) ifac[i] = 1ll*ifac[i]*ifac[i-1]%mod;
    for (ll i = 0; i <= n; i++)
        (ans += 1ll*y[i]*(i == 0 ? 1 : s1[i-1])%mod*s2[i+1]%mod
            *ifac[i]%mod*(((n-i)&1) ? -1 : 1)*ifac[n-i]%mod) %= mod;
    return (ans+mod)%mod;
}
int main(){
	ll n,k;
	cin>>n>>k;
	if(k==0){
		cout<<n<<endl;
		return 0;
	}
	p[0]=0;
	for(ll i=1;i<=k+2;i++) p[i]=(p[i-1]%mod+qpow(i,k))%mod;
	for(ll i=1;i<=k+2;i++) x[i]=i;
	if(n<=k+2){
		cout<<p[n]<<endl;
	}
	else{
		cout<<lagrange(k+2,x,p,n)<<endl;
	}
	return 0;
}

总结：

其实拉格朗日插值在算法竞赛中主要用于数据分析，即对于给定的某些关系构造出若干已知点，然后利用这些已知点去计算通项公式。