Chapter3-1: 矩阵的标准型与特征值计算

Jordan标准型

形如：

$J_{i} = \left[ \begin{matrix} \lambda_{i} & 1 \\ & \lambda_{i} & 1 \\ & & ... \\ & & &\lambda_{i}\\ \end{matrix} \right]_{r_{i} \times r_{i}}$

的矩阵被称为$r_{i}$阶Jordan块。由若干个Jordan块构成的分块对角矩阵成为Jordan标准型：

$J = \left[ \begin{matrix} J_{1} \\ & J_{2} \\ & & J_{3} \\ &&&... \\&&&& J_{s} \end{matrix} \right]$

Jordan定理

设$A \in C^{n \times n}$，则$A$与一个Jordan标准型相似，即存在$P \in C_{n} ^{n \times n}$使得$P^{-1}AP=J$。且这个Jordan标准型除了其中的Jordan块的排列顺序外被$A$唯一决定。则称其为$A$的Jordan标准型，记为$J_{A}$。

Jordan标准型及相似变换矩阵的求解

设$a_{ij}(\lambda)(i=1,2,3…m;j=1,2,3…,n)$，为复数域上的多项式，则以$a_{ij}(\lambda)$为元素的 $m \times n$阶矩阵

$A(\lambda) = \left[ \begin{matrix}a_{11}(\lambda) & a_{12}(\lambda) & ... & a_{1n}(\lambda) \\ ... \\ a_{m1}(\lambda) & a_{m2}(\lambda) & ... & a_{mn}(\lambda)\end{matrix} \right]$

为$\lambda$矩阵或者多项式矩阵。

如果$\lambda$矩阵$A(\lambda)$存在一个$r(r \geq 1)$阶子式为非零多项式，而所有的$r+1$（如果存在）阶子式全为零多项式，则称$A(\lambda)$的秩为$r$，记作:

$\rank(A(\lambda))=r$或者$r_{A(\lambda)}=r$。零矩阵的秩为0。

如果$n$阶矩阵$A(\lambda)$的秩为$n$，则$A(\lambda)$满秩或非奇异，否则称$A(\lambda)$降秩或者奇异的。

初等行变化/列变换

交换两行(列)
用$k(k \neq 0)$数乘某行/列的所有元素
某行(列)的$\varphi(\lambda)$倍加到零一行(列)

如果$\lambda$矩阵$A(\lambda)$经过有限次初等变换变成$\lambda$矩阵$B(\lambda)$，则称$A(\lambda)$与$B(\lambda)$矩阵等价，记作$A \simeq B$。

定理：

任意非零的$\lambda$矩阵$A(\lambda)=(a_{ij}(\lambda))_{m \times n}$等价于如下形式的矩阵：

$A(\lambda) \simeq S(\lambda)=\left( \begin{matrix} d_{1}(\lambda) \\ & d_{2}(\lambda) \\ & & ...\\ &&& d_{r}(\lambda) \\ & & & & ... \\ & & & & & 0 \\ & & & & & & 0 \end{matrix} \right)$

其中$r$为$A(\lambda)$的秩，$d_{i}(\lambda)$是首项系数为1的多项式，且$d_{i}(\lambda)|d_{i+1}(\lambda)(i=1,…,r-1)$。

$S(\lambda)$被称为$A(\lambda)$的Smith标准型，$d_{i}(\lambda)$成为$A(\lambda)$的不变因子。

例题：

求$\lambda$矩阵

$A(\lambda)=\left( \begin{matrix}1-\lambda & 2\lambda-1 & \lambda \\ \lambda & \lambda^2 & -\lambda \\1+\lambda^2 & \lambda^2+\lambda-1 & -\lambda^2 \end{matrix} \right )$

的Smith标准型和不变因子：

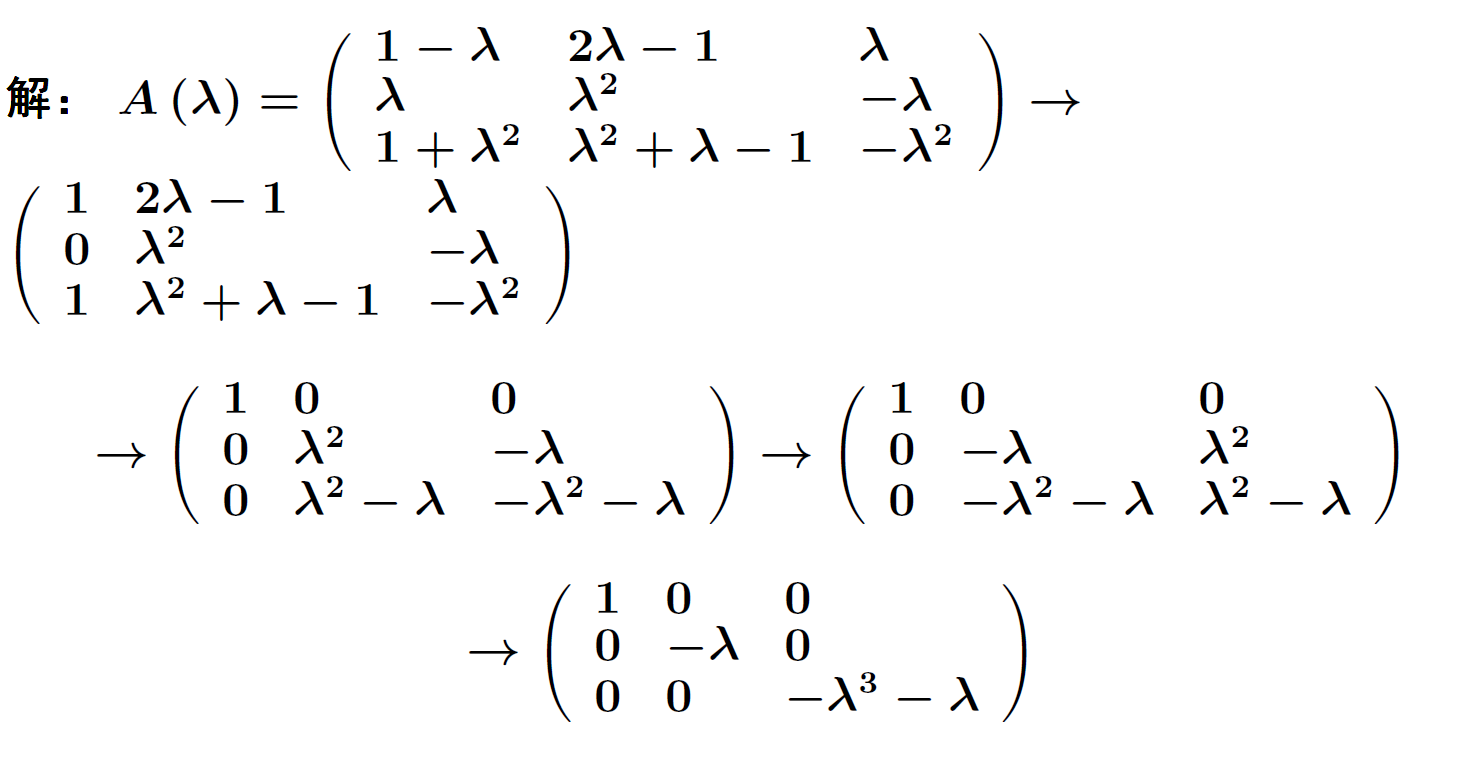
因此所求的Smith标准型为：

$S(\lambda) = \left( \begin{matrix} 1 & 0 & 0 \\ 0 & \lambda & 0 \\ 0 & 0 & \lambda^3+\lambda \end{matrix} \right)$

不变因子为：$d_{1}(\lambda)=1,d_{2}(\lambda)=\lambda,d_{3}(\lambda)=\lambda^3+\lambda$。