Chapter1：距离与范数

距离空间

设 $X$ 是非空集合，对 $X$ 中任意两元素 $x,y$满足，按照某一法则对应唯一的实数$d(x,y)$，且满足下列三条性质：

非负性：$d(x,y) \geq 0$，$d(x,y)=0$当且仅当$x=y$；
对称性：$d(x,y)=d(y,x)$；
三角不等式：$d(x,y) \leq d(x,z)+d(y,z)$. 对所有的$x,y,z \in X$成立.

则称$d(x,y)$为$x,y$的距离，并称$X$是以$d$为距离的距离空间，记作$(X,d)$。

完备性

设$\{x_{n}\}_{n=1}^{\infty}$是距离空间$(X,d)$上的点列，若对于任意的 $\epsilon > 0$，都存在$N \in \mathbb{N}$，当$n,m > N$时有$d(x_{n},x_{m}) < \epsilon$；则称

$\{x_{n}\}_{n}^{\infty}$为Cauchy列。如果$X$中任意Cauchy列都在$X$中收敛，则$X$是完备的。

范数与赋范空间

设$X$是复数域$C$上的线性空间，$0$为$X$的零元素，若对于$X$中每个元素$x$，按照一个法则对应一个实数$||x||$满足：

$||x|| \geq 0$且$||x||=0$当且仅当$x=0$；
$||x+y|| \leq ||x||+||y||$；
$||\alpha x||=|\alpha| \cdot ||x||$；

则称$||x||$为$x$的范数，$X$称为以$||.||$为范数的赋范空间。

向量范数

在$F^{n}$（实或复欧几里得空间）中的向量$x,y$，可以使用$x-y$的范数来描述它们之间的距离。

令$x = (\xi_{1},\xi_{2},…,\xi_{n})^{T} \in C^{n}$，则：

1范数：$||x||_{1} = \sum_{k=1}^{n}|\xi_{k}|$（每一维模长的和）
2范数：$||x||_{2} = \sqrt{\sum_{k=1}^{n}|\xi_{k}|^2}$（每一维模长的平方的和开根）
$\infty$范数：$||x||_{\infty} = max_{k=1}^{n}|\xi_{k}|$（最大的模长）
$p$范数：$||x||_{p} = (\sum_{k=1}^{n}|{\xi_{k}}|^p)^{\frac{1}{p}}(1 \leq p \leq \infty)$

$C^{n}$上所有的向量范数等价。

注：范数等价的一个通俗理解就是可以通过缩放得到其他范数。

以$p=1,2,\infty$和二维向量$v=(x,y)^T$为例，画出其各自的”单位圆“：

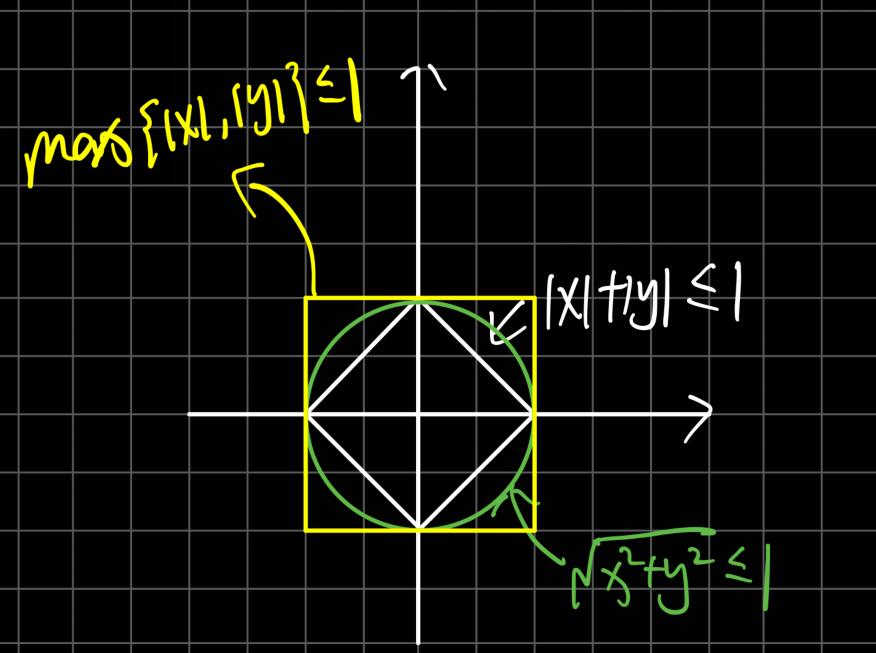
QQ截图20210916095844.jpg

可以轻松的观察到他们之间是可以缩放的。

矩阵范数

如果$C^{n \times n}$上的一个实函数$||.||:C^{n \times n} \rightarrow R$满足：

$||A|| \geq 0$，且$||A||=0$的充要条件为$A=0$
对于$\lambda \in C$有：$||\lambda A|| = |\lambda| \cdot ||A||$
$||A+B|| \leq ||A||+||B||$
$||AB|| \leq ||A|| ||B||$

则称$||.||$是一个矩阵范数，而$||A||$是$C^{n \times n}$上的$A$的矩阵范数。

矩阵范数的分类及计算

若$A = (a_{i,j})_{n \times n} \in C^{n \times n}$，则：

$m_{1}$范数：$||A||_{m_{1}} = \sum_{i=1}^{n}{\sum_{j=1}^{n}}{|a_{i,j}|}$
$m_{\infty}$范数：$||A||_{m_{\infty}} = n \times max_{i,j}{|a_{i,j}|}$
$F$范数：$||A||_{F} = \sqrt{\sum_{i=1}^{n}\sum_{j=1}^{n}|a_{i,j}|^2}=\sqrt{tr(A^HA)}=\sqrt{tr(AA^H)}$

算子范数：

$||A||_{m} = \max\limits_{||x||=1} ||Ax||,A \in C^{n \times n}$

根据算子范数可以诱导出矩阵的$1,2, \infty$范数：

1范数：$||A||_{1} = \max\limits_{j}{\sum_{i=1}^{n}{|a_{i,j}|}}$，极大列和范数
2范数（谱范数）：$||A||_{2} = \sqrt{\lambda_{1}}$,其中$\lambda_{1}$为$A^{H}A$的最大特征值
$\infty$范数：$||A||_{\infty} = \max\limits_{i}{\sum_{j=1}^{n}|a_{i,j}|}$，极大行和范数

矩阵范数与向量范数的相容性

设$||.||_{m}$是$C^{n \times n}$上的矩阵范数，$||.||_{a}$是$C^{n}$上的向量范数，如果对于任意的$A \in C^{n \times n}$和$x \in C^{n}$有：

$||Ax||_{a} \leq ||A||_{m}||x||_{a}$

则向量范数$||.||_{a}$与矩阵范数$||.||_{m}$是相容的。

向量$1$范数与矩阵$m_{1}$范数相容
向量$2$范数与矩阵$F$范数相容
向量$1,2,\infty$范数都与矩阵的$\infty$范数相容

定理：任何向量范数都存在与之相容的矩阵范数（算子范数），任何矩阵范数都存在与之相容的向量范数

酉矩阵

设$A \in C^{n \times n}$，若$A$满足$A^{H}A=I$,则称$A$为酉矩阵。

酉矩阵性质

若$A$是酉矩阵，则$A^{-1},A^{H},A_{T},\overline{A},A^{k}$也是酉矩阵
若$A,B$是酉矩阵，则$AB$也是酉矩阵
若$A$是酉矩阵，则$|det(A)|=1$
$A$是酉矩阵的充要条件是$A$的$n$个列/行向量是标准正交向量组
$A$是酉矩阵的充要条件是对于任意的$\alpha,\beta \in C^{n}$有：$(A\alpha,A\beta) = (\alpha,\beta)$
若$A$是酉矩阵，$\lambda$是$A$的特征值，则$|\lambda|=1$

酉不变性

对于酉矩阵$U,V$有：

$||UA||_{F}=||AV||_{F}=||UAV||_{F}=||A||_{F}$

证明：
$||UA||_{F} = \sqrt{tr((UA)^{H}UA)}=\sqrt{tr(A^HU^HUA)}=\sqrt{tr(A^HA)}=||A||_{F}$
后面也类似。
$||UA||_{2}=||AV||_{2}=||UAV||_{2}=||A||_{2}$

证明：
$||UA||_{2} = \sqrt{\max\limits_{\lambda}((UA)^HUA)} = \sqrt{\max\limits_{\lambda}(A^HA)}=||A||_{2}$
$||AV||_{2} = \sqrt{\max\limits_{\lambda}(V^HA^HAV)} = \sqrt{\max\limits_{\lambda}(A^HA)}= ||A||_{2}$ (矩阵相似性)

Hermite矩阵

对于$A \in C^{n \times n}$，如果：$A^{H}=A$，则$A$是Hermite矩阵，如果$A^{H}=-A$,则$A$是反Hermite矩阵

正规矩阵（十分重要的概念）

若$A \in C^{n \times n}$，如果$A^HA=AA^H$，则$A$是正规矩阵。

如果$A$是正规矩阵，则：$||A||_{2}=\max\limits_{k}|\lambda_{k}|$

证明：

$A$是正规矩阵的充要条件是$A$酉相似于对角矩阵，因此有：

$U^HAU = \left[\begin{matrix}\lambda_{1}& ... &...\\... & \lambda_{2} & ... \\...&...&...\\ ... & ... & \lambda_{n}\end{matrix}\right]$

故：

$A = U\left[\begin{matrix}\lambda_{1}& ... &...\\... & \lambda_{2} & ... \\...&...&...\\ ... & ... & \lambda_{n}\end{matrix}\right]U^H$

因此：

$||A||_{2}=\sqrt{\max\limits_{\lambda}(A^HA)}=\sqrt{\max\limits_{\lambda}(U^H\left[\begin{matrix}\\\overline{\lambda_{1}}& ... &...\\... & \overline{\lambda_{2}} & ... \\...&...&...\\ ... & ... & \overline{\lambda_{n}}\end{matrix}\right]\left[\begin{matrix}\lambda_{1}& ... &...\\... & \lambda_{2} & ... \\...&...&...\\ ... & ... & \lambda_{n}\end{matrix}\right]U) }=\max\limits_{k}|\lambda_{k}|$

Q.E.D

此外正规矩阵还有一些其他的性质：

$||A^H||_{m_{1},F,m_{\infty}}=||A||_{m_{1},F,m_{\infty}}$
$||A^H||_{1,2,\infty} = ||A||_{\infty,2,1}$